Mapping algorithms that rely on registering point clouds inevitably suffer from local drift, both in localization and in the built map. Applications that require accurate maps, such as environmental monitoring, benefit from additional sensor modalities that reduce such drift. In our work, we target the family of mappers based on the ICP algorithm which use additional orientation sources such as the IMU. We introduce a new angular penalty term derived from Lie algebra. Our formulation avoids the need for tuning arbitrary parameters. Orientation covariance is used instead, and the resulting error term fits into the ICP cost function minimization problem. Experiments performed on our own real-world data and on the KITTI dataset show consistent behavior while suppressing the effect of outlying IMU measurements. We further discuss promising experiments, which should lead to optimal combination of all error terms in the ICP cost function minimization problem, allowing us to smoothly combine the geometric and inertial information provided by robot sensors.
Contributions
- The formulation of a novel penalty on the ICP process using Lie algebra, leading to more accurate maps
Results in Images
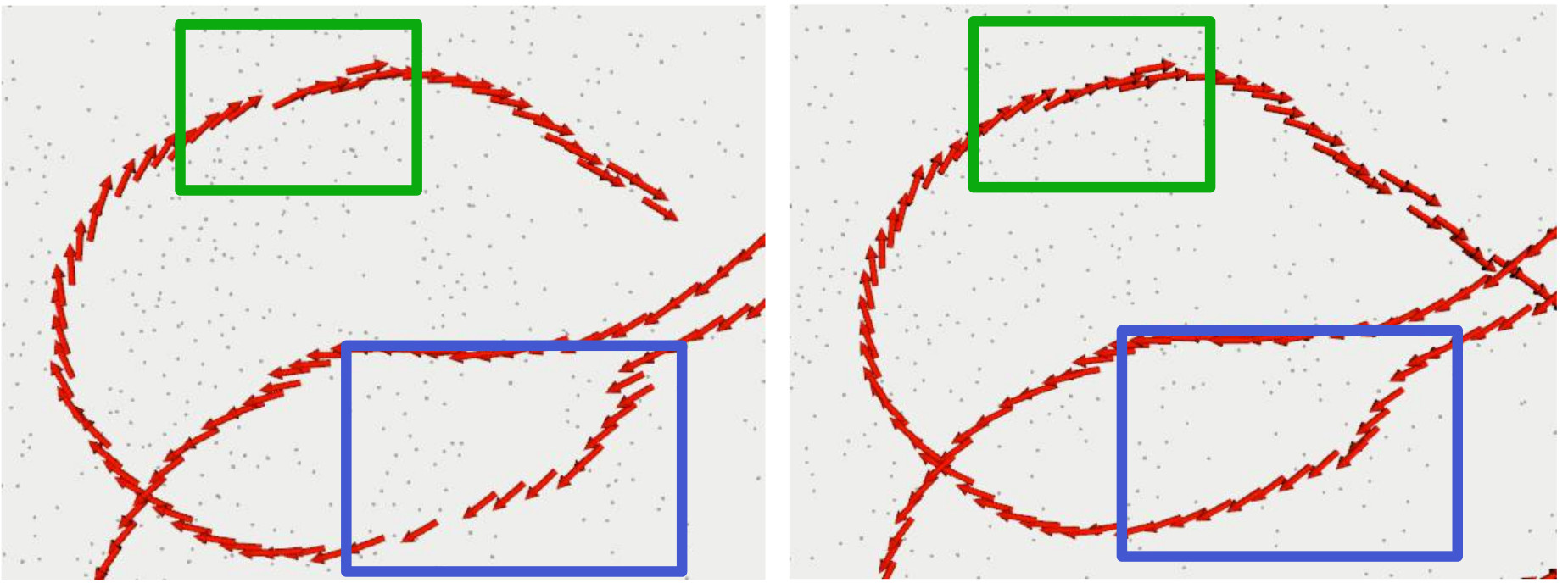
To demonstrate the performance of our method, we tested our algorithm in a snowy environment at the Laval University. During this experiment, the robot was performing high-velocity trajectories: because of the low friction of the snow, the robot was considerably skidding and slipping and thus generating incorrect odometry prior. Due to the high velocity, the distance between subsequent point clouds can be large and with wrong prior, the ICP can fall into local minimum by wandering too far away from the orientation prior. The figure below shows two computed trajectories for the same experiment, with and without our rotational penalty. On the trajectory computed without the penalty (left), two breaking points can be seen at the top and bottom part of the picture, meaning that the ICP converged to a wrong solution. With the Lie penalty (right), these breaking points are avoided as this term pushes the ICP to converge quicker to the right solution while avoiding local minimum.
Reference
Vaidis, M., Laconte, J., Kubelka, V., & Pomerleau, F. (2020). Improving the Iterative Closest Point Algorithm using Lie Algebra. In IROS 2020 Workshop - Bringing geometric methods to robot learning, optimization and control. https://doi.org/10.1109/CRV52889.2021.00012
